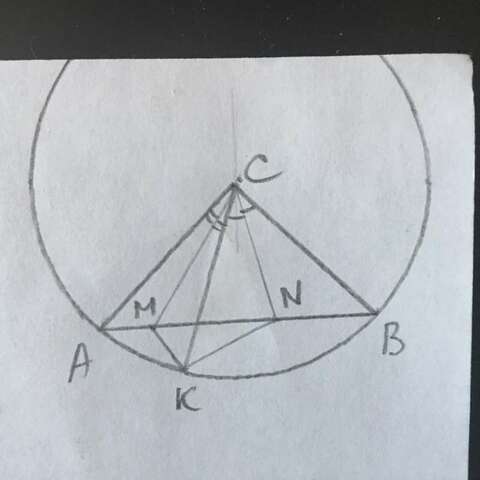
Пусть ∠ВСN=x, ∠АСМ=у.
х+у=45°, значит ∠МСN=45°=х+у.
Из центра в точке С проведём дугу АВ на которой выберем точку К такую, чтобы KN=BN.
Треугольники ВСN и KCN равны по трём сторонам, значит ∠СКN=∠СBN=45°. ∠KCN=∠ВСN=y ⇒ ∠КСМ=х.
Треугольники САМ и СКМ равны т.к. СА=СК, СМ - общая сторона и ∠АМС=∠КСМ, значит ∠СКМ=∠САМ=45° и КМ=АК.
В тр-ке КМN ∠K=90°, значит MN²=KM²+KN²=AM²+BN².
Доказано.