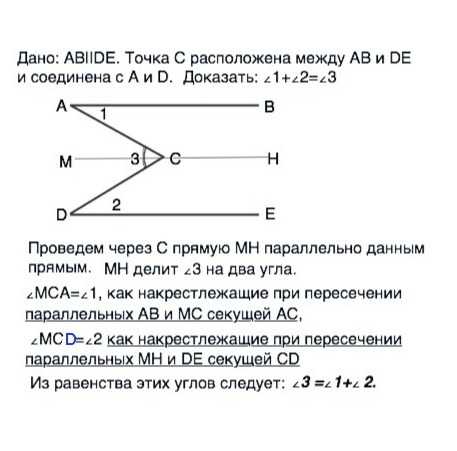
Дано: АВ||DE. Точка С расположена между прямыми АВ и DE и соединена с А и D. Образовавшиеся углы обозначены:
∠ВАС-∠1, ∠ЕDС-∠2, ∠АСD - ∠3
Доказать: ∠1+∠2=∠3
Проведем через С прямую МН параллельно данным прямым. (см. рисунок в приложении).
МН разделит ∠3 на ∠АСМ и ∠DCM .
∠МСА=∠1, как накрестлежащие при пересечении АВ║МС секущей АС, и
∠МCD=∠2 как накрестлежащие при пересечении МН║DE секущей CD.
Из равенства этих углов следует:
∠3 =∠1+∠ 2.