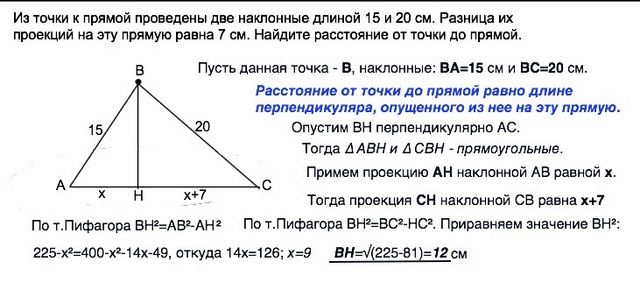
Пусть данная точка - В, наклонные: ВА=15 см и ВС=20 см.
Расстояние от точки до прямой равно длине перпендикуляра, опущенного из нее на эту прямую.
Опустим ВН перпендикулярно АС.
Тогда ∆ АВН и ∆ СВН - прямоугольные.
Примем проекцию АН наклонной АВ равной х.
Тогда проекция СН наклонной СВ равна х+7
По т.Пифагора ВН²=АВ²-АН²
По т.Пифагора ВН²=ВС²-НС². Приравняем значение ВН²:
225-х²=400-х²-14х-49, откуда 14х=126; х=9
ВН=√(225-81)=12
Расстояние от В точки до прямой АС=12 см