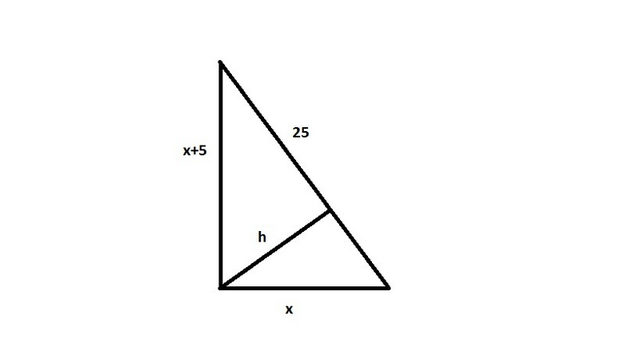
1. Находим длины катетов через теорему Пифагора:
а=х, b=x+5;
x²+(x+5)²=25²;
x²+x²+10x+25=625;
x²+5x-300=0;
D=25+1200=1225, √D=35;
x₁= -20 < 0;
x₂=15
a=15 см;
b=15+5=20;
2. Находим площадь треугольника:
a*b/2=150 см²;
3. Площадь треугольника через гипотенузу и высоту:
с*h/2=150;
h=300/25=12 см.