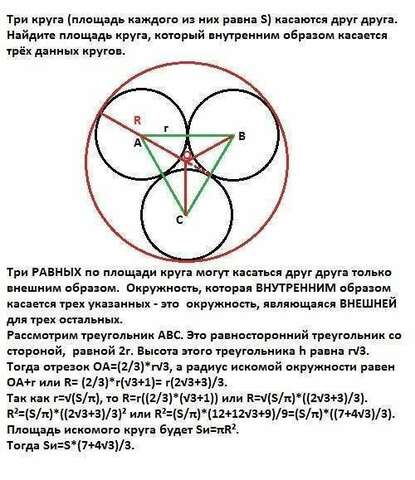
Три РАВНЫХ по площади круга могут касаться друг друга только внешним образом. Окружность, которая ВНУТРЕННИМ образом касается трех указанных - это окружность, являющаяся ВНЕШНЕЙ для трех остальных.
Рассмотрим треугольник АВС. Это равносторонний треугольник со стороной, равной 2r. Высота этого треугольника h равна r√3.
Тогда отрезок ОА=(2/3)*r√3, а радиус искомой окружности равен ОА+r или
R=(2/3)*r(√3+1)= r(2√3+3)/3.
Так как r=√(S/π), то R=r((2/3)*(√3+1)) или R=√(S/π)*((2√3+3)/3).
R²=(S/π)*((2√3+3)/3)² или R²=(S/π)*(12+12√3+9)/9=(S/π)*((7+4√3)/3).
Площадь искомого круга будет Sи=πR².
Тогда Sи=S*(7+4√3)/3.