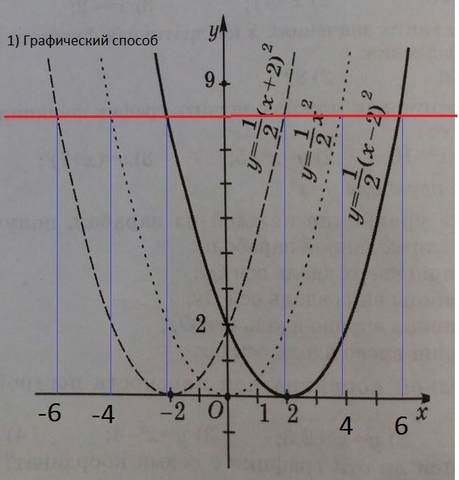
252.
1) Проверка с помощью вычислений y=8:
(1) y=1/2x²; 8=1/2x²; x²=16; x=+-4;
(2) y=1/2(x+2)²; 8=1/2(x+2)²; (x+2)²=16; |x+2|=4; x+2=-4; x=-6; x+2=4; x=2;
(3) y=1/2(x-2)²; 8=1/2(x-2)²; (x-2)²=16; |x-2|=4; x-2=-4; x=-2; x-2=4; x=6.
2)
(1) y=1/2x² - касается оси ОХ в точке (0;0) и симметричен относительно оси OY;
(2) y=1/2(x+2)² - касается оси ОХ в точке (-2;0), не симметричен оси OY;
(3) y=1/2(x-2)² - касается оси ОХ в точке (2;0), не симметричен оси OY.
3)
(1) y=1/2x² - вершина параболы (0;0);
(2) y=1/2(x+2)² - вершина параболы (-2;0), его можно построить сдвигом графика (1) влево на 2 единицы вдоль оси ОХ;
(3) y=1/2(x-2)² - вершина параболы (2;0), его можно построить сдвигом графика (1) вправо на 2 единицы вдоль оси ОХ.
4)
(1) y=1/2x²: а) убывает на промежутке (-∞;0); б) возрастает на промежутке (0;+∞); в) наименьшее значение имеет в точке х=0 (у=0);
(2) y=1/2(x+2)²: а) убывает на промежутке (-∞;-2); б) возрастает на промежутке (-2;+∞); в) наименьшее значение имеет в точке х=-2 (у=0);
(3) y=1/2(x-2)²: а) убывает на промежутке (-∞;2); б) возрастает на промежутке (2;+∞), наименьшее значение имеет в точке х=2 (у=0).