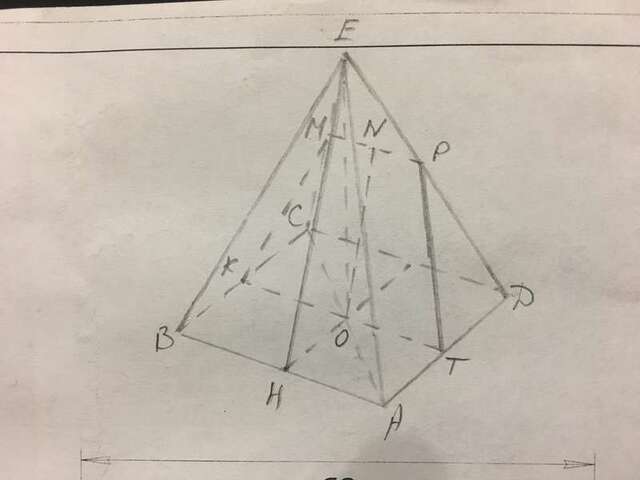
Так как плоскости АВЕ и КМPT параллельны, то АВ║КТ, О∈КТ ⇒ ВК=СК и АТ=ДТ; АЕ║РТ и ВЕ║КМ, значит в треугольниках АЕД и ВЕС отрезки РТ и КМ - средние линии, значит ЕР=ДР и ЕМ=СМ, значит МР - средняя линия треугольника СЕД ⇒ МР=СД/2=12/2=6 см.
КТ║СД, МР║СД ⇒ МР║КТ, значит КМPT - трапеция, причём равнобедренная (в равных тр-ках АЕД и ВЕС средние линии КМ и РТ равны).
В трапеции КМPT КМ=ВЕ/2, РТ=АЕ/2, МР=АВ/2 и все прямые соответственно параллельны, значит высота трапеции NO равна половине высоты тр-ка АЕВ. NO=EH/2.
В прямоугольном тр-ке ЕОН ОН=АВ/2=12/2=6 см. ЕН²=ЕО²+ОН²=8²+6²=100.
ЕН=10 см.
NO=10/2=5 см.
Площадь искомого сечения: S(KMРТ)=NO·(КТ+МР)/2=5(12+6)/2=45 см² - это ответ.