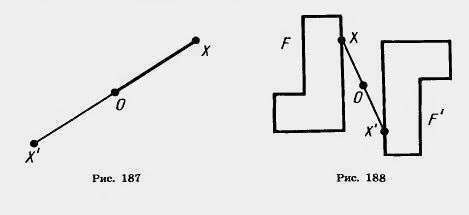
Пусть О — фиксированная точка и X — произвольная точка плоскости (рис. 187). Отложим на продолжении отрезка ОХ за точку О отрезок ОХ', равный ОХ.
Точка X' называется симметричной точке X относительно точки О. Точка, симметричная точке О, есть сама точка О. Очевидно, что точка, симметричная точке X', есть точка X.
Преобразование фигуры F в фигуру F', при котором каждая ее точка X переходит в точку X', симметричную относительно данной точки О, называется преобразованием симметрии относительно точки О. При этом фигуры F и F' называются симметричными относительно точки О (рис. 188).
Симметрия относительно точки