1. Михаил в электронной таблице в ячейках С1, С2, С3 и С4 записал целые числа. В ячейке...

Question

93 просмотров

1. Михаил в электронной таблице в ячейках С1, С2, С3 и С4 записал целые числа. В ячейке В1 он хочет получить произведение этих чисел, если все числа положительны, сумму этих чисел, если среди них есть хотя бы одно отрицательное, и 0 в остальных случаях. Чтобы получить требуемый результат, в ячейку В1 Миша должен записать формулу:
а) = ЕСЛИ (МАКС (С1:С4) < 0; СУММ (С1:С4) ; ПРОИЗВЕД (С1:С4) )
б) = ЕСЛИ (МИН (С1:С4) > 0; ПРОИЗВЕД (С1:С4) ; СУММ (С1:С4) )
в) = ЕСЛИ (ПРОИЗВЕД (С1:С4) < 0; СУММ (С1:С4) ; ПРОИЗВЕД (С1:С4) )
г) = ЕСЛИ (МИН (С1:С4) < 0; СУММ (С1:С4) ; ПРОИЗВЕД (С1:С4) )

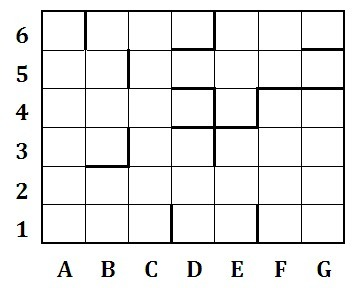
2. Исполнитель Робот перемещается по клеточному полю (см.влож. 1), переходя из клетки в клетку по соответствующей команде: вверх, вниз, вправо, влево. Между некоторыми клетками поля установлены перегородки, сквозь которые Робот пройти не может. Также Робот умеет проверять условие отсутствия стены у каждой стороны клетки, в которой он находится.
Робот, находясь на поле, изображённом на рисунке, исполняет следующий алгоритм:
Делать пока (не справа стена)
{
Вправо
Вниз
}
Делать пока (не сверху стена)
{
Вверх
Вправо
}
При успешном исполнении алгоритма длиной пути Робота считается количество переходов из клетки в соседнюю клетку. Робот начинает исполнение алгоритма в одной из перечисленных клеток. Укажите, для какой из этих клеток путь Робота окажется самым длинным.
а) B2 б) B6 в) D5 г) A5

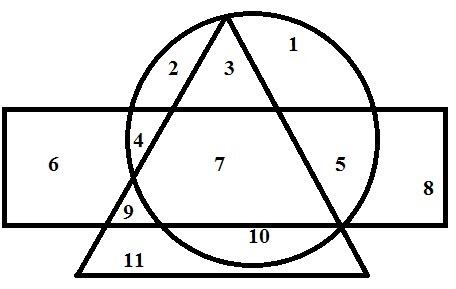
3. Пусть дано три пересекающиеся фигуры: круг, треугольник и прямоугольник. Числами обозначены непересекающиеся области, на которые разбиваются эти фигуры при указанном на рисунке (влож. 2) взаимном расположении.
Пусть высказывание А - «Точка принадлежит кругу», В - «Точка принадлежит треугольнику», через С - «Точка принадлежит прямоугольнику». Найдите области, для которых будет истинным выражение
(¬ А ~ В) ∧ С ∨ А ∧ (С ~ В)
В ответе укажите числа в порядке возрастания (без пробелов и каких-либо знаков препинания), например 1234.

Информатика Sashaariefiev_zn (2.4k баллов) 10 Май, 18 | 93 просмотров

Дан 1 ответ

Правильный ответ

1) Я в Excel не очень разбираю, но считаю, что ответ "Б" эквивалентен ответу "Г"

2) Начиная из клеток вариантов "А" и "Б" робот упирается в стену во время выполнения алгоритма. Начиная из клетки A5 робот выйдет за пределы поля, а начиная из клетки D5, робот перейдет 6 раз. => Ответ: "В".

3) Выражение (¬ А ~ В) ∧ С ∨ А ∧ (С ~ В)
//PascalABC.Net 3.2
//выход(ответ): 4568
var
s:string;
a, b, c: boolean;

function f(n: integer):boolean;
begin
case n of
1 : s:='к';
2 : s:='к';
3 : s:='кт';
4 : s:='кп';
5 : s:='кп';
6 : s:='п';
7 : s:='ктп';
8 : s:='п';
9 : s:='пт';
10: s:='кт';
11: s:='т';
end;
a:='к' in s;
b:='т' in s;
c:='п' in s;
result:=(not a and not b) and c or a and (c and not b);
end;

begin
for var i:=1 to 11 do if f(i) then write (i);
end.

Студэнt_zn (3.8k баллов) 10 Май, 18