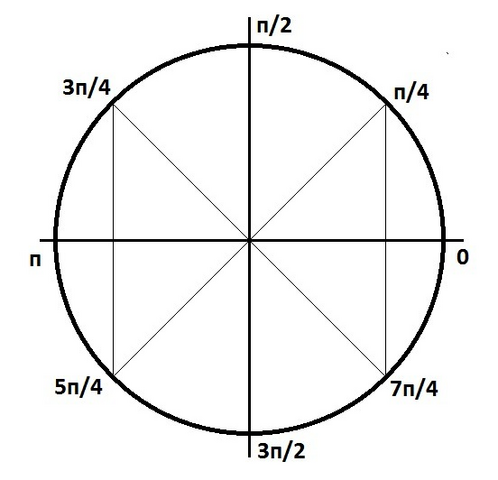
1. Круг в приложении. Второй и третий корни можно объединить в один, первый остаётся без изменений:

2. Перебор значений целочисленного параметра n производится тогда, когда задан отрезок, которому должны принадлежать корни. В задании отрезок не указан.
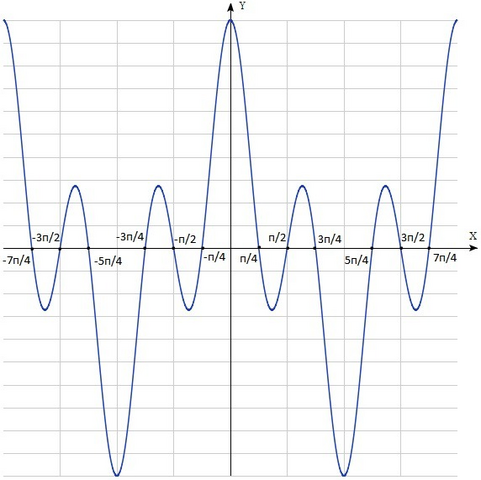
3. График в приложении.