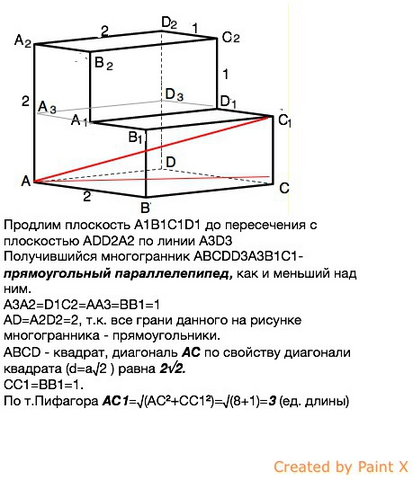
Найдите расстояние между вершинами А и С1 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Т.к. все углы многогранника прямые, все ребра многоугольника перпендикулярны основаниям и плоскость А1В1С1D1 параллельна плоскости АВСD.
Продлим плоскость А1В1С1D1 до пересечения с плоскостью АDD2A2 по линии А3D3
Получившийся многогранник АBCDD3A3B1C1- прямоугольный параллелепипед, как и меньший над ним.
А3А2=D1C2=AA3=BB1=1
АD=A2D2=2, т.к. все грани данного на рисунке многогранника - прямоугольники.
ABCD - квадрат, диагональ АС по свойству диагонали квадрата (d=a√2 ) равна 2√2.
СС1=ВВ1=1.
По т.Пифагора АС1=√(AC²+CC1²)=√(8+1)=3 (ед. длины)