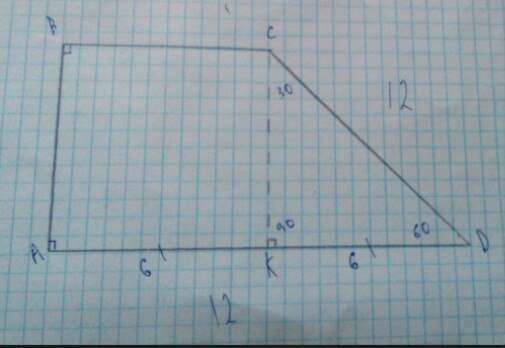
Дано:
ABCD - прямоуг. трапеция
∠A = ∠B = 90°
∠D = 60°
AD = DC = 12
Найти P
Решение:
∠С = 360° - (90° · 2 + 60) = 120°
Проведем высоту CK на большее основание, ∠K = 90°
Рассмотрим треугольник CKD - прямоугольный, ∠KCD = 180° - (90° + 60°) = 30° => по теореме, катет лежащий напротив ∠ в 30° = 1/2 гипотенузы => KD = 6 => AK = 12 - 6 = 6
Рассмотрим четырехугольник ABCK, тк ∠A = ∠B = ∠C = ∠K = 90° => ABCK - квадрат, AK = AB = BC = CK = 6
P = 6+6+12+12 = 36