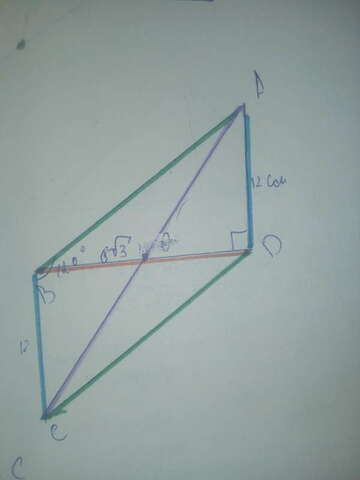
∠CBD = ∠ADB = 90° - как накрест лежащие.
∠ABD = ∠B - ∠CBD = 120° - 90° = 30°. Тогда AD = 1/2AB => AB = 2AD = 24 см.
По теореме Пифагора:
BD = √AB² - AD² = √24² - 12² = √576 - 144 = √432 = 12√3 см.
OC = OA, BO = OD, т.к. диагонали точкой пересечения делятся пополам. BO = 6√3 см.
AD = BC = 12 см, т.к. противоположные стороныр параллелограмма равны.
По теореме Пифагора:
CO = √CB² + BO² = √144 + 108 = √252 = 6√7 см.
CA = 2CO = 12√7 см.
SCOD = 1/2CB•OD = 1/2•12см•6√3см = 36√2 см².
Оьвет: 12√3 см, 12√7 см, 36√3 см².