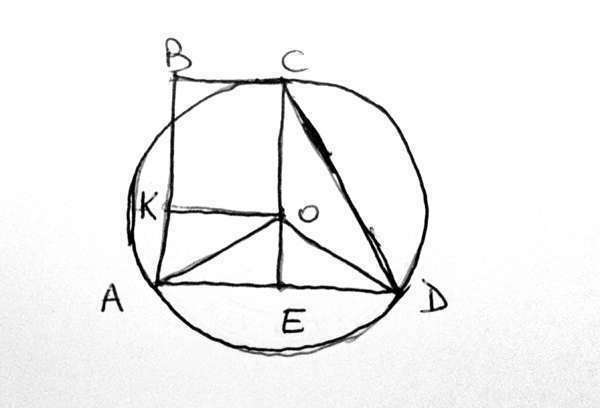
Как известно, касательная перпендикулярна радиусу, проведенному в точку касания. Поэтому из угла трапеции С можно провести через центр окружности О отрезок СЕ до стороны АD, перпендикулярный основаниям трапеции ВС и AD. Проведем также отрезок ОК из центра окружности О до стороны АВ, параллельный основаниям трапеции ВС и AD. Соединим также центр окружности О с вершинами А и D.
Рассмотрим треугольник AOD. Он равнобедренный, т.к. АО=DO=R - радиусу окружности.В этом треугольнике ОЕ - высота, а значит биссектрисса <АОК = 90 - <AOE = 90-60 = 30.<br>Т.к. ВСОК - прямоугольник, то ВС=КО и ВК=СО=R.
Из прямоугольного треугольника АКО:
R = АО = КО/Cos30 = BC/(√3/2) = 2BC/√3.
С учетом того, что по условиям задачи сторона АВ больше радиуса окружности, AB = AK+BK = R*SinПримечание: если отрезок АВ был бы меньше радиуса окружности, то его можно было бы найти из выражения АВ=ВК-АК = R-AK.