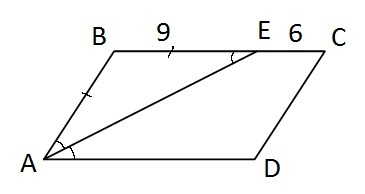
Пусть ABCD - параллелограмм, АЕ - биссектриса ∠BAD, отрезок ВЕ=9 см, ЕС=6 см. ΔАВЕ - равнобедренный (∠EAD=∠AEB - внутренние накрест лежащие углы при параллельных AD и BC и секущей АЕ), значит АВ=ВЕ=9 см. Так как противолежащие стороны параллелограмма равны, то AB=CD=9 см, BC=AD=9+6=15 (см).
Р=2(АВ+ВС)=2*(9+15)=2*24=48 (см).
Ответ: 48 см.