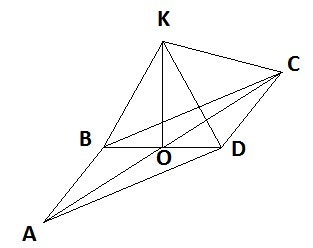
Дано:
ABCD - ромб.
AB = 5 см.
BD = 6 см.
OK ⊥ ABCD.
Найти KA, KB, KC, KD.
Решение:
О - точка пересечения диагоналей. Значит AO = CO, BO = DO = 3 см.
Рассмотрим треугольники BOK и DOK. Они оба прямоугольные, т.к. OK - перпендикуляр. Сторона OK общая, BO = DO. Значит, эти треугольники равны и KB = KD. Из треугольника BOK по т. Пифагора
KB = √(64+9) = √(73) см.
Найдём диагональ AC. Сумма квадратов диагоналей ромба равна квадрату стороны, умноженному на 4.
AC^2+BD^2 = 4*AB^2
AC^2 +36 = 4*25
AC^2 = 64
AC = 8 см.
Тогда AO =CO = 4 см.
Треугольники AKO и CKO равны, т.к. прямоугольные, KO - общая сторона, AO = CO. Из треугольника CKO по т. Пифагора
KC = √(64+16) = √(80) см.