Изобразите на координатной плоскости множество решений уравнения |y^2-x^2|=y-x
-----------------
| y² - x² |= y - x ;
| y - x |*| y + x | = y - x
необходимое ограничение : y-x ≥ 0 ⇔ y ≥ x ⇒ | y - x | = y - x
( y - x )*| y + x | = y - x ;
( y - x ) ( | y + x | -1) =0 ;
---------------------------
{ y ≥ x ; ( y - x ) ( | y + x | -1) =0 ⇔{ y ≥ x ; [ y - x = 0 ; y + x = -1 ; y + x = 1. ⇔
[ { y ≥ x ; y - x = 0 . { y ≥ x ; y = - x - 1 . { y ≥ x ; y = - x +1 .
(равносильно совокупности трех систем уравнений) .
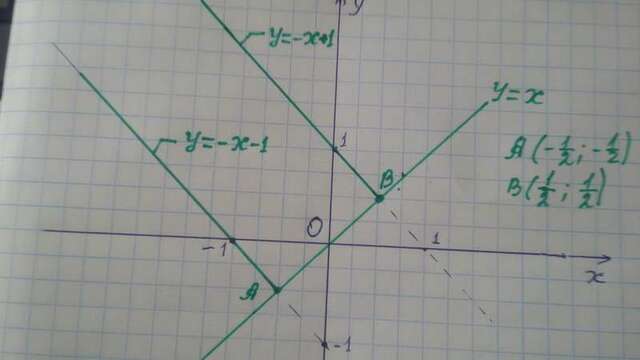
Множество решений уравнения |y^2-x^2|=y-x →объединение прямой y = x и двух лучей с началами в точках A(-1/2 ; -1/2) и B(1/2;1/2) точки
пересечения прямой y = x соответственно с y = - x - 1 и y = - x + 1 ;
прямые y = x и y = - x ± 1 перпендикулярны k₁*k₂ = 1 *(-1) = -1 ) .