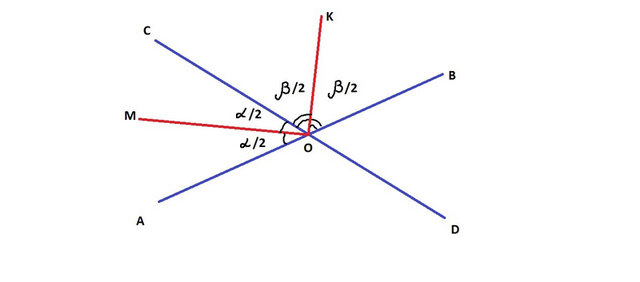
Пусть ∠АОС=α; ∠COB=β, тогда
∠AOM=∠MOC=α/2 (так как ОМ-биссектриса)
и ∠СОК=∠КОВ=β/2
∠АОС и ∠COB, образуют развернутый угол АОВ, следовательно
α+β=180°
разделим это уравнение на два
α+β=180° |:2
(α/2)+(β/2)=90°
(α/2)+(β/2)=∠MOC+∠СОК=∠MOK=90°
Ответ: Да, ∠MOK будет прямым.