Метод индукции - от простого к сложному.
При n =1 и n=2 - просто нет фигур.
Пусть n= 3 - треугольник - диагоналей нет - N = 0 - без рисунка.
Усложняем.
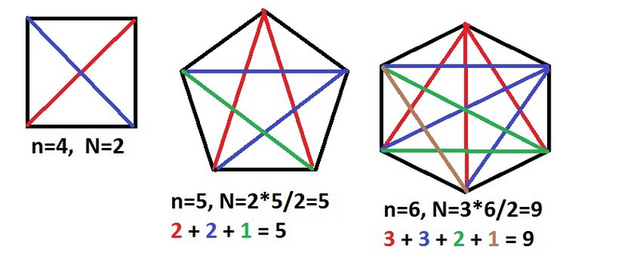
n=4 - квадрат - две диагонали - N = 2 - рисунок
n =5 - пятиугольник - делаем рисунок.
Диагонали можно провести к вершинам, кроме тех двух, что на соседних ребрах
N= (n-3) - для начала. Всего вершин у нас = n, НО ... диагоналей в два раза меньше, потому, что будут повторяться - от А к В и от В к А.
Вот и получается формула числа диагоналей:
N = (n-3) *n : 2 - ЧТД - что и требовалось доказать.
И, на всякий случай, проверка для n=6 - по формуле - 9 диагоналей и на рисунке 9 диагоналей.