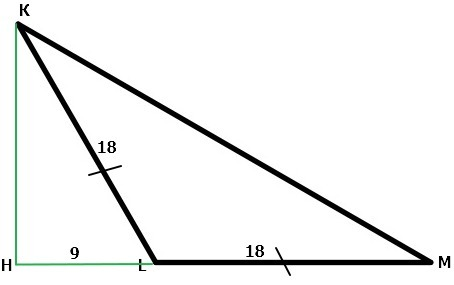
Дано: ΔKLM: KL = LM = 18, KH - высота, LH = 9.
Найти: cos ∠KLM
Решение:
1. Рассмотрим ΔKHL, т.к. KH - высота ⇒ ∠KHL = 90°
2. Т.к. HL = 9, а KL = 18, то получаем, что HL = 1/2 * KL ⇒ по обратной теореме (если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30°) ∠HKL = 30°
3. ∠KHL + ∠HLK + ∠HKL = 180°
∠HLK = 180° - (∠KHL + ∠HKL) = 180° - (90° + 30°) = 60°
4. ∠HLK и ∠KLM - смежные ⇒ ∠HLK + ∠KLM = 180° ⇒ ∠KLM = 180° - ∠HLK = 180° - 60° = 120°
5. cos ∠KLM = cos 120° = cos (180° - 60°) = -cos 60° = -1/2
Ответ: cos ∠KLM = -1/2