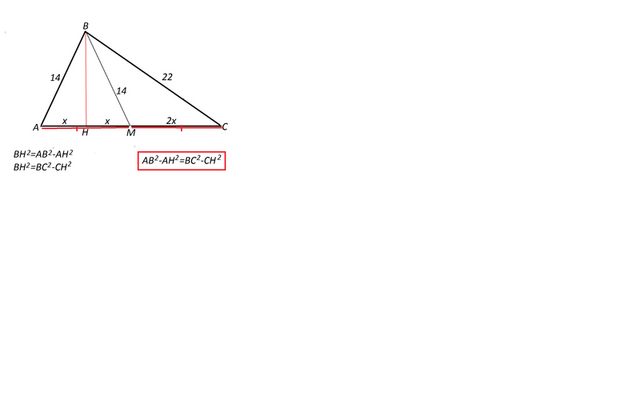
Пусть вершины треугольника будут А,В,С,
медиана ВМ=АВ=14 см,
ВС=22 см
Так как медиана равна одной из боковых сторон, она образует с этой стороной равнобедренный треугольник, основание которого - половина ∆ АВС.
Опустим на АС высоту ВН.
В равнобедренном треугольнике высота еще и медиана. АН=НМ
Обозначим АН=х.
Тогда АС=4х, НС=3х
Из прямоугольных треугольников АВН и ВСН выразим по т. Пифагора высоту ВН
ВН²=АВ²-АН² ВН²=ВС²-НС²
АВ²-АН²= ВС²-НС²
196-х²=484-9х²
8х²= 288
х²=36
х=6 см
АС=4х=24 см
Р∆ АВС=14+24+22= 60 см