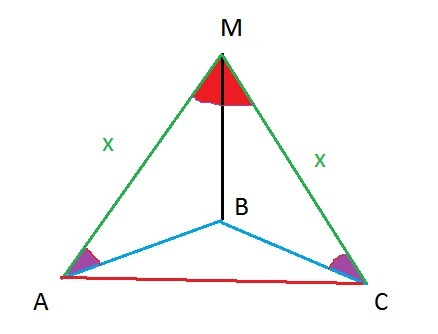
∠МАВ=∠МСВ=α
катет МВ- общий
Прямоугольные треугольники МАВ и МВС равны по катету МВ и острому углу ∠МАВ=∠МСВ=α)
Из равенства прямоугольных треугольников следует равенство наклонных.
Пусть АМ=МС=х.
Равные наклонные имеют равные проекции.
АВ=СВ=х·сosα.
Из треугольника АМС по теореме косинусов:
АС²=АМ²+МС²-2АМ·МС·сosβ=x²+x²-2x²cosβ
Пусть в треугольнике АВС ∠АВС=γ,
по теореме косинусов
АС²=АВ²+ВС²-2АВ·ВС·cosγ=
=x²cos²α+x²cos²α-2x²cos²α·cosγ
Приравниваем правые части
x²+x²-2x²cosβ=x²cos²α+x²cos²α-2x²cos²α·cosγ ⇒
сosγ=(2x²cos²α-2x²+2x²cosβ)/2x²cos²α;
сosγ=(cos²α-1+cosβ)/(cos²α).