ДАНО
Y = 6/(3x+2)
ИССЛЕДОВАНИЕ
1. Область определения - непрерывность.
3х + 2 ≠ 0 и х ≠ - 2/3.
Х∈(-∞, -2/3]∪[-2/3,+∞).
2. Пересечение с осью абсцисс - Х.
х∈∅ - корней нет.
3. Пересечение с осью ординат - У.
х=0, У(0) = 3.
4. Поведение в точке разрыва - х = -2/3
Слева - Y= -∞ и справа - Y=+∞.
5. Поведение функции на бесконечности.
lim(-∞) = 0 lim(+∞) = 0.
6. Наклонная асимптота - У=0.
7. Исследование на четность.
Y(x) = 6/(3x+2)
Y(-x) = - 6/(3x-2)
Функция ни чётная ни нечетная.
8. Производная функции.
Y' = -18/(3x+2)².
9. Поиск экстремумов - Y' = 0. Корней нет. Х∈∅.
10. Монотонность функции.
Убывает - Х∈(-∞, -2/3]
Возрастает - X∈[-2/3, +∞).
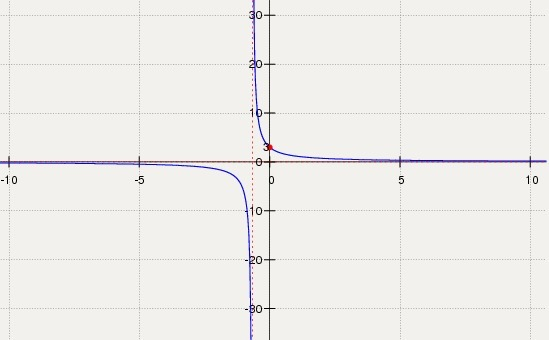
11. График прилагается.