Исследовать функцию и построить график y=x*ln(x)

$f(x)=x\ln x$

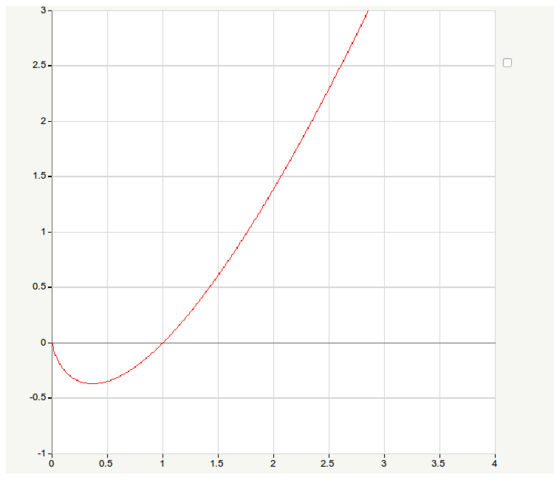
При x стремящемся к нулю функция стремится к нулю, а в бесконечности уходит на бесконечность.

$f'(x)=\ln x +1$

Отсюда находим точку минимума: x=1/e. На отрезке от 0 до 1/e функция убывает от 0 до (-1/e), а после возрастает до бесконечности.

$f''(x)=\frac1 x$

то есть функция выпукла вниз.