Cos(2x) = cos(x)^2 - sin(x)^2 = 2 * cos(x)^2 - 1
Возводим в квадрат, подставляем в числитель и упрощаем его, приводя подобные члены и используя простые тригонометрические формулы. После проведенных преобразований получаем, что числитель равен
sin(x)^2 * ( 4 * cos(x)^2 - 1)
Таким образом, предел нам нужно найти следующей функции при x -> 0:
sin(x)^2 * ( 4 * cos(x)^2 - 1)/x^2 = (sin(x)/x)^2 * ( 4 *cos(x)^2 - 1).
Предел произведения равен произведению пределов, если пределы сомножителей есть и конечны.
lim(sin(x)/x), x -> 0 равен 1
lim(4 *cos(x)^2 - 1), x -> 0 равен 3
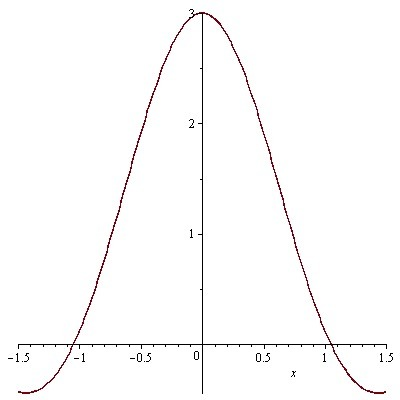
Ответ: предел указанной функции при x ->0 равен 3. В приложенном файле график функции :) (для наглядности).