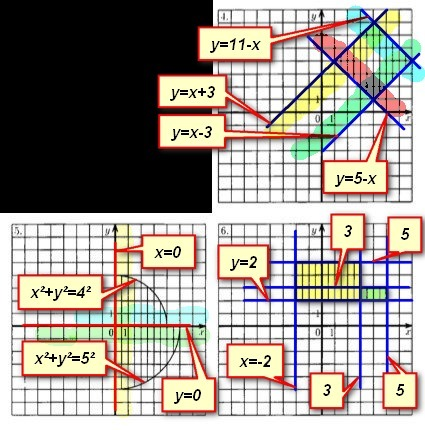
Во вложении - раскрашенная для пояснения решения картинка.
Главное в таких задачах - правильно составить условие попадания в заштрихованную область, а затем построить по нему корректное логическое выражение.
Не совсем корректная постановка задачи требует сделать одно допущение. Нам не указали, входят ли в заштрихованные области их границы. Будем считать, что входят и на этом основании все отношения будет нестрогими (т.е.составленными при помощи ≤ и ≥). Если границы контуров входить не должны, отношения строятся строгими и содержат операции < и >.
Первое, с чего нужно начать - составить уравнения линий, описывающих контуры. Это чистая математика и разбирать тут процесс нахождения уравнений таких линий смысла я не вижу.
Далее, нужно руководствоваться очевидным: если нужная нам область лежит "выше" или на линии контура, описанного уравнением вида y=f(x), то такая область описывается в виде y ≥ f(x). Аналогично, область расположенная "ниже" или на линии такого контура описывается в виде y ≤ f(x)
Задание 4
"Желтая" область y≤x+3, "зеленая" y≥x-3, "красная" y≥5-x, "голубая" y≤11-x.
Все эти четыре условия должны выполняться одновременно, поэтому их связываем логическим "И" (конъюнкцией):
(y≤x+3) ∧ (y≥x-3) ∧ (y≥5-x) ∧ (y≤11-x)
Соответственно, в языке программирования (далее рассматриваем паскаль) это логическое выражение запишется в виде
(y<=x+3) and (y>=x-3) and (y>=5-x) and (y<=11-x)<br>
Задание 5
Здесь два круговых сектора, расположенных в I и IV координатных четвертях. Уравнение окружности в декартовых координатах хорошо известно: x²+y²=R², где К - радиус окружности.
I четверть образуется пересечением "желтой" и "голубой" зон, т.е.
(x≥0) ∧ (y≥0). И в этой четверти располагается сектор с уравнением
x²+y²=4² ⇒ x²+y²=16. В итоге получаем (x≥0) ∧ (y≥0) ∧ (x²+y²≤16)
Аналогично в IV-й, "желто-зеленой" четверти пишем
(x≥0) ∧ (y≤0) ∧ (x²+y²≤25). Осталось объединить эти области по ИЛИ", т.е. точка может попадать или в одну область, или в другую, но не в обе одновременно.
((x≥0) ∧ (y≥0) ∧ (x²+y²≤16)) ∨ ((x≥0) ∧ (y≤0) ∧ (x²+y²≤25))
Тут можно сделать небольшое упрощение, вынеся за скобки (x≥0).
(x≥0) ∧ (((y≥0) ∧ (x²+y²≤16)) ∨ ((y≤0) ∧ (x²+y²≤25))).
Вспоминаем, что операция ∧ "старше" чем ∨ и это позволяет избавиться от лишней пары скобок.
(x≥0) ∧ ((y≥0) ∧ (x²+y²≤16) ∨ (y≤0) ∧ (x²+y²≤25))
На паскале:
(x>=0) and ((y>=0) and (x*x+y*y<=16) or (y<=0) and (x*x+y*y<=25))<br>
Задание 6
Здесь сложный контур, который мы можем разбить на два прямоугольника и свести задачу к аналогичной предыдущей.
"Желтый" прямоугольник описывается набором условий
(x≥-2) ∧ (x≤3) ∧ (y≥2) ∧ (y≤5)
Зеленый прямоугольник
(x≥3) ∧ (x≤5) ∧ (y≥2) ∧ (y≤3)
И здесь следует объединение по "ИЛИ":
((x≥-2) ∧ (x≤3) ∧ (y≥2) ∧ (y≤5)) ∨ ((x≥3) ∧ (x≤5) ∧ (y≥2) ∧ (y≤3))
Можно вынести за скобки y≥2
(y≥2) ∧ ((x≥-2) ∧ (x≤3) ∧ (y≤5) ∨ (x≥3) ∧ (x≤5) ∧ (y≤3))
И на паскале:
(y>=2) and ((x>=-2) and (x<=3) and (y<=5) or (x>=3) and (x<=5) and (y<=3))<br>
Только теперь можно написать программу - все остальное, по сути, к информатике отношения не имело и это как раз одна из причин по которой информатика оказывается в школе одним из самых сложных предметов: при решении задач приходится привлекать самые разные знания из других предметов - математики, физики, экономики и т.д.
Программа для задания 4
var
x,y:real;
begin
Write('Введите через пробел координаты точки (x,y): ');
Read(x,y);
Writeln((y<=x+3) and (y>=x-3) and (y>=5-x) and (y<=11-x))<br>end.
Пример программы
Введите через пробел координаты точки (x,y): 3.1 3.4
True
Остальные две программы пишутся совершенно аналогично: вставляем логическое выражение, составленное для паскаля, в процедуру Writeln():
Для задания 5:
Writeln((x>=0) and ((y>=0) and (x*x+y*x<=16) or (y<=0) and (x*x+y*y<=25)))<br>
Для задания 6:
Writeln((y>=2) and ((x>=-2) and (x<=3) and (y<=5) or (x>=3) and (x<=5) and (y<=3)))<br>