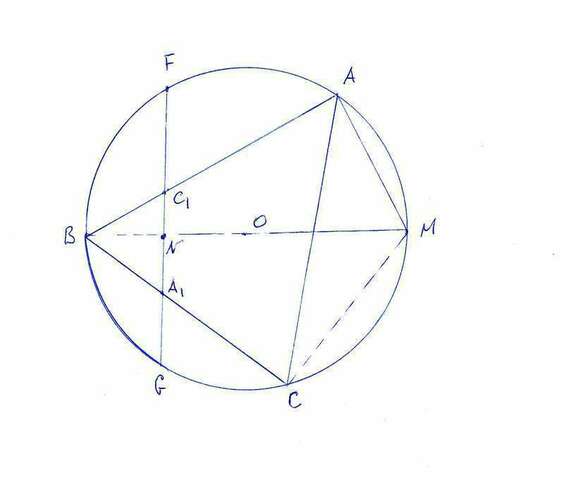
См чертеж. О - центр описанной окружности, ВМ - диаметр, перпендикулярный FG (из за равенства дуг FB и BG), N - середина FG.
Треугольники ВС1N и BAM подобны (прямоугольные с общим острым углом), поэтому BN/BC1 = BA/MB; или BN*MB = BC1*BA;
точно так же из подобия BNA1 и BCM BN*MB = BA1*BC;
можно, конечно, теперь начать вычислять отрезки, а можно заметить, что получилось BC1/BC = BA1/BA = 2/5; (ясно, что ВС1 = 2); то есть треугольники АВС и А1ВС1 подобны с коэффициентом подобия 2/5;
(Это довольно полезная штука, можно и запомнить - прямая, перпендикулярная радиусу описанной окружности, проведенному в вершину треугольника, отсекает от треугольника ему же подобный треугольник.)
Если обозначить площадь АВС как S, то площадь A1BC1 равна S*(2/5)^2;
а площадь четырехугольника AC1A1C равна S*(1 - (2/5)^2) = 21*S/25;
Остается найти площадь АВС по формуле Герона (например), она равна 6√6
(повторю из предыдущей задачи
p = (5 + 6 + 7)/2 = 9; p - 5 = 4; p - 6 = 3; p - 7 = 2;
S^2 = 9*4*3*2; S = 6√6;)
Ответ 126√6/25;