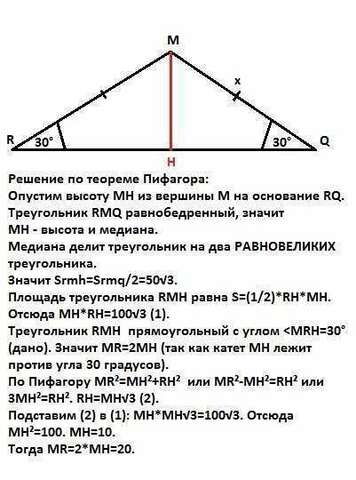
Решение по теореме Пифагора:
Опустим высоту MH из вершины M на основание RQ.
Треугольник RMQ равнобедренный (MR=RQ - дано), значит
MH - высота и медиана.
Медиана делит треугольник на два РАВНОВЕЛИКИХ треугольника.
Значит Srmh=Srmq/2=50√3.
Площадь треугольника RMH равна S=(1/2)*RH*MH. Отсюда MH*RH=100√3 (1).
Треугольник RMH прямоугольный с углом По Пифагору MR²=MH²+RH² или MR²-MH²=RH² или
3MH²=RH². RH=MH√3 (2).
Подставим (2) в (1): МН*MH√3=100√3. Отсюда
МН²=100. МН=10.
Тогда MR=2*MH=20.