3 вариант
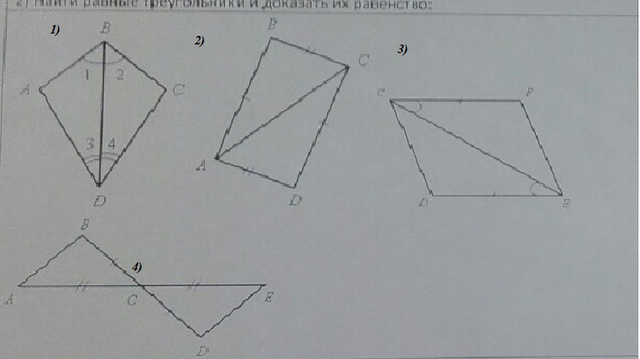
1-й признак - По двум сторонам и углу между ними.(4 рисунок)
АС=СЕ;ВС=СD;∠АСВ=∠DСЕ (вертикальные).⇒ΔАСВ=ΔЕСD
2-й признак - По стороне и прилежащим к ней углам.(3 рис.) и (1 рис.)
(в 3 рис.)тк АВСD параллелограмм, то ∠DСЕ=∠СЕF (тк ∠DEC=∠ECF , а противолежащие углы у параллелограмма равны⇒∠DСЕ=∠СЕF)⇒ΔCDE=ΔEFC
(в 1 рис.) тк∠1=∠2, ∠3=∠4, а BD- общая сторона, то ΔDAB=ΔDCB (по 2-му признаку)
3-й признак - по 3-м сторонам.(2 рис.) тк AB=DC, AD=BC, а АС- общая, то ΔАВС=ΔCDA
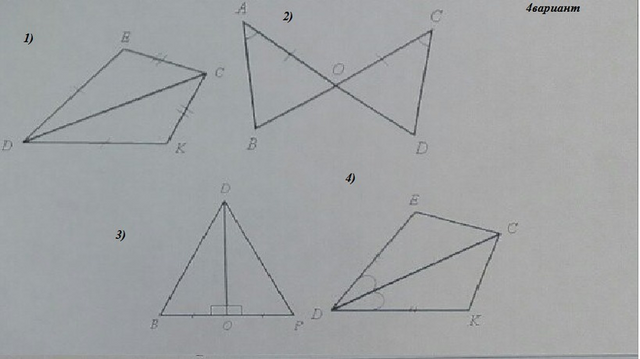
4 Вариант
(1 рис.) тк DE=DK, KC=EC,а CD- общая сторона, тоΔDEC=ΔDKC (по 3-му признаку)
(2 рис.) тк АО=ОС, ∠ВАО=∠DCO,а ∠BOA=∠DOA(вертикальные) ΔBAO=ΔDCO(по 2-му признаку)
(3 рис.) тк BO=OF, ∠BOD=∠DOF, OD- общая сторона, то⇒ ΔBOD=ΔDOF(по 1-му признаку), но так как этот ΔBDF равнобедренный, то ΔBOD=ΔDOF (и по 3-му признаку).
4(рис.)тк ∠EDC=∠CDK, DK=DE, а DC-общая сторона, то ΔCDE=ΔCDR (по 1-му признаку)