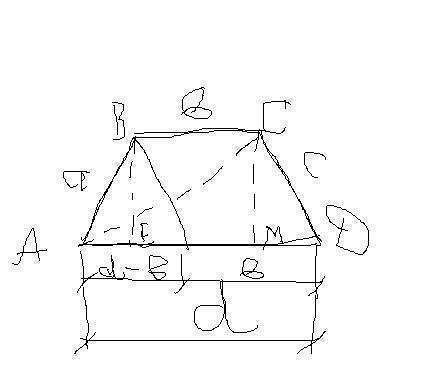
Для нахождения объема призмы нужно знать площадь её основания и высоту.
Площадь трапеции в основании равна произведению высоты на среднюю линию.
Высота трапеции равна высоте треугольника АВК, где ВК =с. а АК=d-b=17cm.
h=(2V(p(p-a)(p-c)(p-(d-b)))/(d-b)=(2V(34(34-26)(34-25)(34-17))/17=24 см.
Lср=39+22/2=30,5 см. So=24*30,5=732 cm^2
Высоту призмы можно найти, разделив площадь сечения
АА1С1С на диагональ АС.
Если провести вторую высоту СМ, получим два прямоугольных
треугольника – АСМ и СМД.
ДМ = V(c^2-h^2)=V(25^2-24^2)=7 cm. AM=39-7=32 cm.AC=V(32^2+24^2)=V(1024+576)=40 cm.
Высота призмы равна 400/40=10 см.
Объём прихмы равен 732*10=7320 см^3.