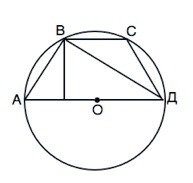
Вписать в окружность можно только равнобедренную трапецию.
Если центр такой окружности лежит на большем основании, то угол, образованный боковой стороной и диагональю, равен 90°, т.к. опирается на диаметр ( большее основание).
Обозначим трапецию АВСД.
ВС=12, АД=20.
ВН - высота.
Высота прямоугольного треугольника, опущенная из тупого угла, делит основание на отрезки, меньший из которых равен полуразности оснований, больший - их полусумме. ⇒
АН=(АД-ВС):2=(20-12):2=4
ДН=(АД+ВС):2=16
Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу. Другими словами, квадрат высоты равен произведению отрезков, на которые она делит гипотенузу.
ВН²=АН•ДН
ВН=√(4•16)=8
Площадь трапеции равна произведению высоты на полусумму оснований.
Ѕ=8•16=128 (ед. площади)