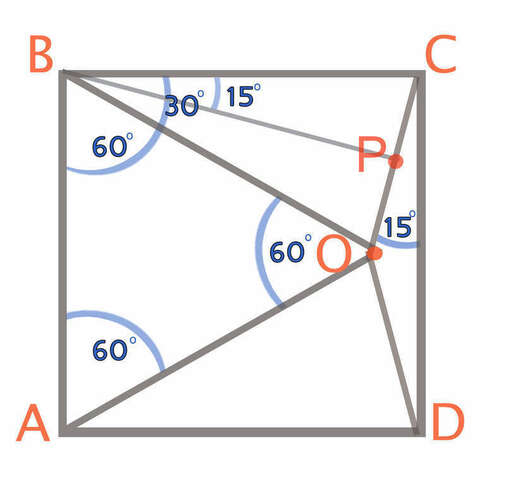
Предположим, что равносторонний Δ АВО уже существует.
Достроим его до квадрата ABCD, одна из сторон которого АВ совпадает с одной из сторон Δ АВО. Таким образом мы получим три равнобедренных треугольника: Δ СОD (острые углы которого нам якобы неизвестны) и 2 одинаковых равнобедренных треугольника со сторонами ВО и АО и острым ∠30 °(являющимся частью ∠=90° квадрата, минус ∠=60° Δ-ка АВО).
И если мы опустим высоту в Δ ОВС на сторону ОС, мы разделим Δ ОВС на 2 ∠ по 15° (и получим точку Р на стороне ОС - cм рисунок).
ДЛЯ УГЛОВ С ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫМИ СТОРОНАМИ СПРАВЕДЛИВО УТВЕРЖДЕНИЕ: ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ УГЛЫ РАВНЫ ИЛИ В СУММЕ СОСТАВЛЯЮТ 180°, А ЕСЛИ ЭТИ взаимно перпендикулярные УГЛЫ ОЧЕВИДНО ОСТРЫЕ - ТАКИЕ УГЛЫ безоговорочно РАВНЫ.
Угол РВС взаимно ⊥ углу ОСD, так как BC ⊥ СD как стороны, образующие ∠BCD квадрата, а ВР ⊥ ОС как высота треугольника ОВС. Взаимно перпендикулярные острые углы равны, значит ∠ ОСD =15°, как и ∠ РВС, являющийся половиной ∠ ОВС=30°.
Очевидно, что любое изменение размеров ∠∠ ОСD и ОDC приведёт к тому, что Δ АВО перестанет быть равносторонним. Следовательно Δ АОВ является равносторонним только если ∠∠ ОСD и ODC равны 15 °,