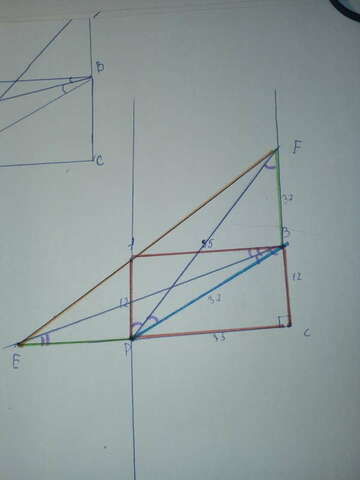
AD || FC => ∠ADF = ∠DFB - как накрест лежащие
∠ADF = ∠FDB
Значит, ∠DFB = ∠BDF => ∆FBD - равнобедренный. Тогда FB = BD.
По теореме Пифагора:
BD = √BC² + AB² = √35² + 12² = √1225 + 144 = √1369 = 37 => FB = 37.
AB||EC => ∠ABE = ∠DEB - как накрест лежащие.
∠ABE = ∠DBE
Значит, ∠DBE = ∠DEB => ∆DEB - равнобедренный. Тогда DE = DB = 37.
FC = FB + BC = 37 + 12 = 49.
EC = ED + DC = 37 + 35 = 72.
По теореме Пифагора:
FE² = FC² + EC² = 49² + 72² = 2401 + 5184 = 7585.
Ответ: 7585.