Пожалуйста!!! Вычислите площади фигур, ограниченных линиями..

1. Найдем точки пересечения графиков функции.
х³=х
х³-х=0
х(х²-1)=0
х(х-1)(х+1)=0
х₁=0 х₂=-1 х₃=1

2.
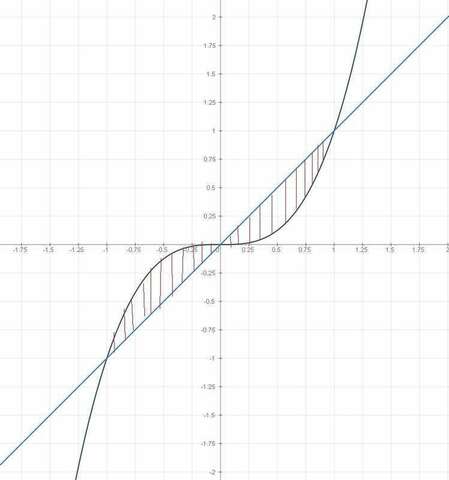
Построим графики и определим какой график находится выше другой.
y=x - прямая
х₁=0 у₁=0
х₂=-2 у₂=-2
х₃=2 у₃=2

у=х³ это кубическая парабола с центром симметрии х=0 у=0.
при х<0 у<0<br>при х>0 у>0
x₁=-1 y₁=-1
x₂=1 y₂=1

3.
Из графиков видно, что на промежутке от [-1; 0] выше х³, а на промежутке [0; 1] выше х.

4.
$S= \int\limits^0_{-1} {(x^3-x)} \, dx +\int\limits^1_{0} {(x-x^3)} \, dx= (\frac{x^4}{4}- \frac{x^2}{2})|_{-1}^0+( \frac{x^2}{2} - \frac{x^4}{4})|_0^1 = \\ \\ ((0- \frac{1}{4})-(0- \frac{1}{2})+(( \frac{1}{2}-0)-(( \frac{1}{4}-0))= \frac{1}{4}+ \frac{1}{4}= \frac{1}{2}$
площадь фигуры ограниченной линиями