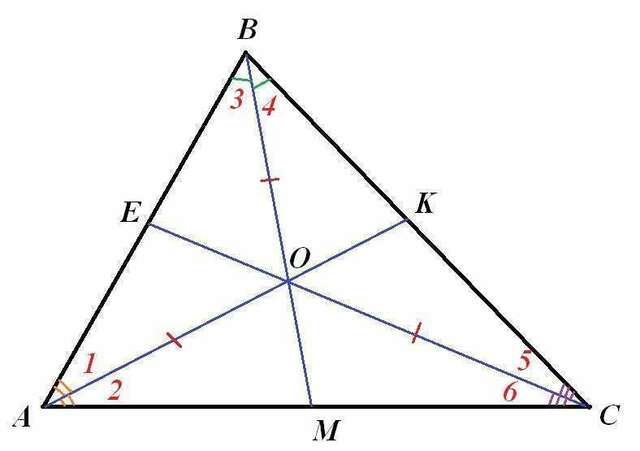
Чертеж во вложении.
Т.к. АК-биссектриса ∠А, то ∠1=∠2.
Т.к. ВМ-биссектриса ∠В, то ∠3=∠4.
Т.к. СЕ-биссектриса ∠С, то ∠5=∠6.
По условию ОА=ОВ=ОС. Значит, треугольники АОВ, АОС и ВОС - равнобедренные.У них в каждом углы при основании равны, т.е.
∠1=∠3, ∠2=∠6, ∠4=∠5. Отсюда следует, что ∠1=∠2=∠3=∠4=∠5=∠6.
Тогда ∠1+∠2 =∠3+∠4= ∠5+∠6, т.е. ∠А=∠В=∠С.
В треугольнике против равных углов лежат равные стороны. Значит, АВ=ВС=АС.
Т.е. ∆АВС - равносторонний. Доказано.