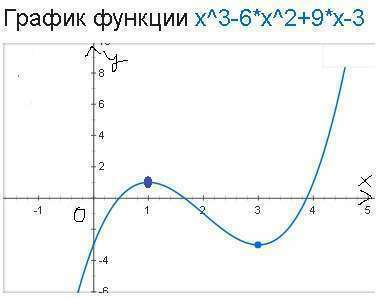
Найдем производную y'
у'=3x²-12x+9
экстремумы в точках где производная =0
y'=0
3x²-12x+9=0 разделим на 3
х²-4х+3=0 найдем корни квадратного уравнения
методом подбора ищем корни среди делителей 3, подходят 1 и 3 можно найти корни через дискриминант но это долго
в точках х=1 и х=3 экстремумы
при х∈(1;3) например х=2 у'=4-8+3=-1 y'<0, у убывает<br>при х∈(-∞;1) например х=-2 у'=4+4+3>0 , y возрастает
при х∈(3, +∞) например х=4 у'=16-16+3>0 , y возрастает
если производная меняет знак с + на - то в этой точке максимум функции
если производная меняет знак с - на + то в этой точке минимум функции
значит в точке х=1 максимум, в точке х=3 минимум
схематический чертеж на рисунке