Около окружности описана трапеция. Докажите, что концы боковой стороны трапеции и центр...

Question

Около окружности описана трапеция. Докажите, что концы боковой стороны трапеции и центр окружности являются вершинами прямоугольного треугольника. Докажите также, что произведение отрезков боковой стороны, на которые она разделена точкой касания, равно квадрату радиуса окружности.

Очень надо!!!!

Answer 1

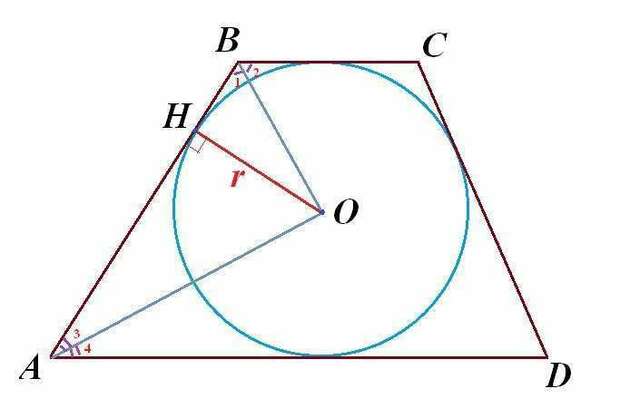
Чертеж во вложении.
Пусть Н-точка касания окружности и боковой стороны АВ трапеции АВСД.
Т.к. окружность вписанная,то ВО - биссектриса ∠В, а АО- биссектриса ∠А.
Поэтому ∠1=∠2 и ∠3=∠4.
Т.к. ВС||АД и АВ-секущая, то ∠А + ∠В=180°, т.к. они односторонние.
∠А=2∠3, ∠В=2∠1
∠А + ∠В=2(∠1 + ∠2)=180° => ∠1 + ∠2=90°
Тогда в ∆АВС  ∠С =180° - (∠1 + ∠2) = 180° - 90° = 90°.
Значит, ∆АВС - прямоугольный.

Теперь в прямоугольном ∆АВС отрезок ОН - радиус вписанной окружности. Тогда ОН⊥АВ, значит, ОН - высота ∆АВС.
По свойству высоты прямоугольного треугольника, проведенной к гипотенузе, получим  AH*BH=r^2" alt="AH*BH=OH^2\ => AH*BH=r^2" align="absmiddle" class="latex-formula">
Доказано.

---