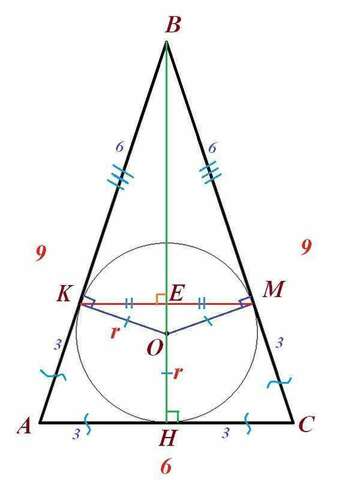
Чертеж во вложении.
Опускаю всякие доказательства равенства треугольников и, как следствие, из соответствующих элементов. Все это можно рассмотреть на чертеже.
Т.к. О-центр впис.окружночти, то ВН-биссектриса, медиана, высота ∆АВС. Значит, АН=СН=3.
По свойству отрезков касательных из одной точки к окружности АН=АК=СН=СМ=3, тогда ВК=ВМ=9-3=6.
Из подобия ∆ВКЕ и ∆ВАН следует
 \frac{6}{9}=\frac{KE}{3}\ => KE=2\\\\ KM=2KE=2*2=4" alt="\frac{BK}{BA}=\frac{KE}{AH}\ => \frac{6}{9}=\frac{KE}{3}\ => KE=2\\\\ KM=2KE=2*2=4" align="absmiddle" class="latex-formula">
\frac{6}{9}=\frac{KE}{3}\ => KE=2\\\\ KM=2KE=2*2=4" alt="\frac{BK}{BA}=\frac{KE}{AH}\ => \frac{6}{9}=\frac{KE}{3}\ => KE=2\\\\ KM=2KE=2*2=4" align="absmiddle" class="latex-formula">
Ответ: 4