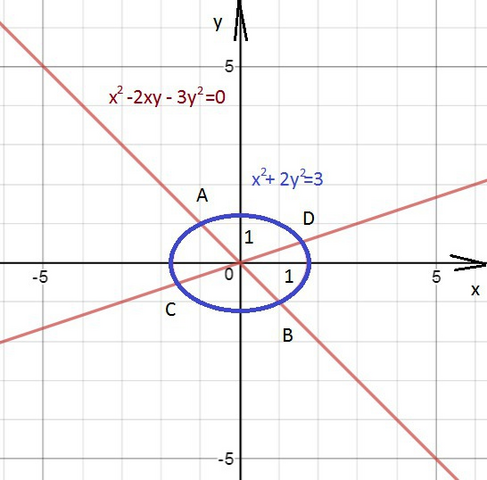
{x²-2xy-3y²=0
{x²+2y²=3
Решаем первое уравнение.
Это однородное уравнение второй степени.
Делим на y².
Замена переменной
х/у=t,
t²-2t-3=0
D=4+12=16
t=-1 или t=3
x=-y или х=3у
Совокупность двух систем
{x=-y
{x²+2y²=3
{x=3y
{x²+2y²=3
Решаем каждую систему способом подстановки
{x=-y {x=1 {x=-1
{(-у)²+2y²=3 ⇒ у²=1 ⇒ {у=-1 или у=1
{x=3y {x=3·√(3/11) {x=-3·√(3/11)
{(3у)²+2y²=3 ⇒ 11у²=3⇒ {y=√(3/11) или {у=-√(3/11)
О т в е т. (1;-1) (-1;1) (3√(3/11) ;√(3/11) ) (-3√(3/11) ; -√(3/11) )
См. графическое решение в приложении.
И второй способ
x²-2ху-3у²=0
х²-2ху+у²-4у²=0
(х-у)²-(2у)²=0
(х-у-2у)·(х-у+2у)=0
(х-3у)·(х+у)=0
Та же совокупность двух систем
{x-3y=0
{x²+2y²=3
{x+y=0
{x²+2y²=3