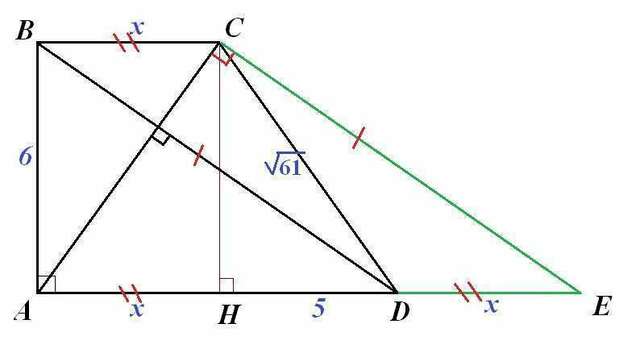
Чертеж - во вложении.
1) Через точку С проведем прямую, параллельную диагонали ВД. Пусть Е - точка пересечения этой прямой и продолжения основания АД.
Т.к. ВС||ДЕ и ВД||СЕ, то ДВСЕ - параллелограмм. Поэтому СЕ=ВД и ВС=ДЕ.
Т.к. АС⊥ВД и ВД||СЕ, то АС⊥СЕ, поэтому ∆АСЕ - прямоугольный.
2) Опустим высоту СН. Тогда АВСН-прямоугольник и СН=АВ=6, АН=ВС.
Тогда в прямоугольном ∆СНД по теореме Пифагора

3) Пусть ВС=х, тогда АД=х+5, АЕ=2х+5.
4) В ∆ВАД по теореме Пифагора 
5) В ∆АBC по теореме Пифагора 
6) В ∆АCE по теореме Пифагора
 " alt="AE^2=AC^2+CE^2,\ CE^2=BD^2\ =>" align="absmiddle" class="latex-formula">
" alt="AE^2=AC^2+CE^2,\ CE^2=BD^2\ =>" align="absmiddle" class="latex-formula">

х=-9 - не удовлетворяет условию.
Значит, ВС = 4, АД = 4 + 5 = 9.
Ответ: 4 и 9.