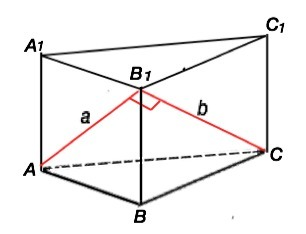
Объем призмы равен произведению площади основания на высоту. Высота прямой призмы равна боковому ребру.
V=S(ABC)•B1B
Ѕ(АВС)=АВ•ВС•sin(АВС):2
Для удобства вычисления переведем длины сторон в дециметры.
АВ=4 дм, ВС=6 дм
Ѕ (АВС)=(4•6•√3/2):2=6√3 дм²
По т.косинусов
АС²=АВ²+ВС²-2АВ•ВС•cos120°
AC*=16+36-2•24•(-1/2)⇒
AC²=76
Из прямоугольного треугольника АВ1С
АВ1²+В1С²=АС²=76
Примем АВ1=а, СВ1=b, тогда а²+b²=76
Выразим квадрат высоты ВВ1 из прямоугольных треугольников АВВ1 и СВВ1 и приравняем выражения.
ВВ1²=а²-16
ВВ1²=b²-36⇒
а²-16=b²-36 ⇒
b²-a²=20
составим систему
 сложим оба уравнения. и получим
сложим оба уравнения. и получим
2b²=96, откуда b²=48
Из ∆СВВ1 по т.Пифагора
h=ВВ1=√(48-36)=2√3
V=6√3•2√3=36 дм²=3600 см²