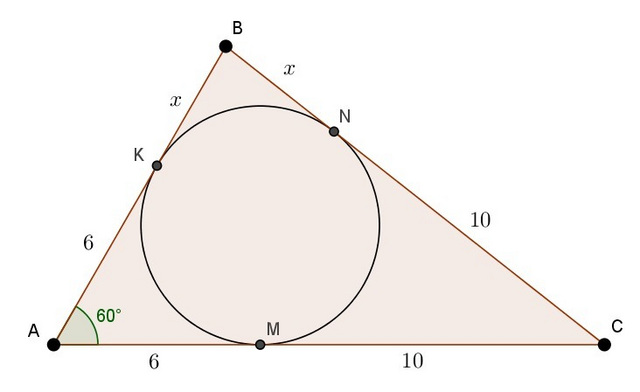
Отрезки касательных, проведённых из одной точки к окружности, равны. Поэтому (см. рисунок) AK = 6, CN = 10, BK = BN = x.
Запишем теорему косинусов для этого треугольника:
BC^2 = AB^2 + AC^2 - 2 AB AC cos A
(x + 10)^2 = (x + 6)^2 + 16^2 - 2 (x + 6) * 16 * 1/2
x^2 + 20x + 100 = x^2 + 12x + 36 + 256 - 16x - 96
20x + 100 = -4x + 36 + 160
24x = 96
x = 4
P = 2(x + 10 + 6) = 2 * 20 = 40