Дана электрическая цепь. Сила тока в первом резисторе 4 А. Найти показания амперметра.

Question

Дано ответов: 2

Правильный ответ

ТРЕТИЙ СПОСОБ:

В ветке амперметра стоит довольно большое сопротивление, так что через него будет течь довольно слабый ток, к которому будет присоединяться ток из R5 идущий вниз.

Будем считать положительным направлением тока I5 – направление вниз. Если предложение неоправданно – мы просто будем иметь отрицательное значение для I5.

Итак: по всем сопротивлениям токи текут либо налево, либо вниз.

I3 = I4 + I5 ;

I2 = I1 + I5 ;

Общее падение напряжения на R3 и R5
равно падению напряжения на R1:

R3 I3 + R5 I5 = R1 I1 ;

Общее падение напряжения на R5 и R2
равно падению напряжения на R4:

R5 I5 + R2 I2 = R4 I4 ;

Подставляем в эти два уравнения
полученные выше выражения для токов:

R3 ( I4 + I5 ) + R5 I5 = R1 I1 ;
R5 I5 + R2 ( I1 + I5 ) = R4 I4 ;

R3 I4 + R3 I5 + R5 I5 = R1 I1 ;
R5 I5 + R2 I1 + R2 I5 = R4 I4 ;

R3 I4 + ( R3 + R5 ) I5 = R1 I1 ; || * R4
( R5 + R2 ) I5 + R2 I1 = R4 I4 ; || * R3 , и складываем:

R4 ( R3 + R5 ) I5 + R3 ( R5 + R2 ) I5 + R3 R2 I1 = R4 R1 I1 ;

( R4 ( R3 + R5 ) + R3 ( R5 + R2 ) ) I5 = ( R4 R1 – R3 R2 ) I1 ;

I1 = I5 ( R3*R4 + R4*R5 + R5*R3 + R2*R3 ) / ( R4 R1 – R3 R2 ) – перемножается попарно внешняя звёздочка R3, R4 и R5 и ещё внешняя диагональ R2*R3 ;

Аналогично:
I4 = I5 ( R1*R2 + R2*R5 + R5*R1 + R2*R3 ) / ( R4 R1 – R3 R2 ) – перемножается попарно внешняя звёздочка R1, R2 и R5 и ещё внешняя диагональ R2*R3 ;

I4/I1 = ( R1*R2 + R2*R5 + R5*R1 + R2*R3 ) / ( R3*R4 + R4*R5 + R5*R3 + R2*R3 ) ;

I4/I1 = ( 2 + 6 + 3 + 4 ) / ( 12 + 18 + 6 + 4 ) = 15/40 ;

I4 = [15/40] I1 ≈ [15/40] 4 ≈ 1.5 А ;

ЧЕТВЁРТЫЙ СПОСОБ (облегчённый третий):

I3 = I4 + I5 ;
I2 = I1 + I5 ;

R3 I3 + R5 I5 = R1 I1 ;
R5 I5 + R2 I2 = R4 I4 ;

2R ( I4 + I5 ) + 3R I5 = R I1 ;
3R I5 + 2R ( I1 + I5 ) = 6R I4 ;

2 I4 + 2 I5 + 3 I5 = I1 ;
3 I5 + 2 I1 + 2 I5 = 6 I4 ;

2 I4 + 5 I5 = I1 ;
5 I5 + 2 I1 = 6 I4 ; вычитаем:

2 I4 – 2 I1 = I1 – 6 I4 ;

8 I4 = 3 I1 ;

I4 = [3/8] I1 ≈ [3/8] 4 = 1.5 А .

logophobia2_zn (137 баллов) 08 Май, 18

Так что третий способ, на мой взгляд, более выгоден с точки зрения общности. Мы же не выделяем каждый раз при решении квадратного уравнения полный квадрат – мы просто пользуемся общим диофантовым решением с дискриминантом. Первый способ тут – в самом деле, тяжеловат, но в некоторых других случаях (например, когда нужно выразить ток одного элемента через общий ток) – он как раз пронзительно короток.

оставил комментарий logophobia_zn (7.5k баллов) 08 Май, 18

Как проводить такой фокус с другими птичками, и т.п. Опять же: общность и зубодробительная прямолинейность подхода – самый верный способ в любом случае добиваться результата, даже если решение не удаётся построить в виде «фокуса». Это к разнице между третьим и четвёртым способом. Третий обладает большей общностью. Для любых аналогичных цепей с другими коэффициентами при R – формула уже готова, и не нужно снова решать систему, хоть и менее громоздкую, как в четвёртом коротком способе.

оставил комментарий logophobia_zn (7.5k баллов) 08 Май, 18

«На переднем крае науки/искусства спереди» – краткость сестра таланта. Согласна. Если же хочется разжевать до мелкой кашицы двухсотлетнюю школьную задачу, то, возможно – не всегда так. Краткость, особенно когда она приводит к верному результату – эффектна и поразительна, краткость подобна фокусу: сначала птички нет – а потом «о-ля-ля» и птицка есть :–) Но для многих фокус так и остаётся неясным, куда делась птичка, откуда взялась птичка.

оставил комментарий logophobia_zn (7.5k баллов) 08 Май, 18

logophobia_zn · Answer 1 · 2018-05-08T14:08:24+0000

ПЕРВЫЙ СПОСОБ:

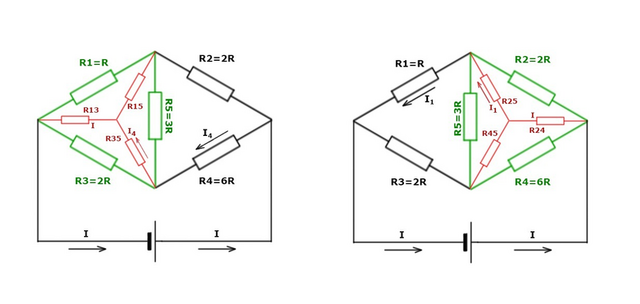
Сначала смотрим на левую схему, приложенную к решению задачи:

Сопротивления R1, R3 и R5 (отмечены зелёным) образуют трёх-контактный омический элемент R135,

Внутри R135 между контактами вокруг R1 – общее сопротивление: 1/[1/R+1/(2R+3R)] = [5/6]R .

Внутри R135 между контактами вокруг R3 – общее сопротивление: 1/[1/[2R]+1/(R+3R)] = [4/3]R .

Внутри R135 между контактами вокруг R5 – общее сопротивление: 1/[1/[3R]+1/(R+2R)] = [3/2]R .

Изменим схему на эквивалентную. Удалим все зелёные резисторы и поставим на их место красные R13, R15 и R35, чтобы они обеспечивали такое же омическое поведение элемента R135, а именно, чтобы:

R13 + R15 = [5/6] R ; [1]

R13 + R35 = [4/3] R ; [2]

R15 + R35 = [3/2] R ; [3]

Вычтем из последнего второе:

R15 – R13 = [1/6] R ;

Сложим это с первым:

R15 = R/2 ;

Из первого:

R13 = R/3 ;

Из второго:

R35 = R ;

На верхнем правом плече эквивалентной схемы: R15 + R2 = 2.5 R ;
На нижнем правом плече эквивалентной схемы: R35 + R4 = 7 R ;
Значит, ток на нижнем плече эквивалентной и исходной схемы будет обратно пропорционален сопротивлению, т.е. будет:

I4 = I [2.5R/9.5R] = [5/19] I ;

Теперь смотрим на правую схему, приложенную к решению задачи:

Сопротивления R2, R4 и R5 (отмечены зелёным) образуют трёх-контактный омический элемент R245. Внутри R245: между контактами вокруг R2 – общее сопротивление: [18/11]R , между контактами вокруг R4 – [30/11]R , между контактами вокруг R5 – [24/11]R .

Изменим схему на эквивалентную. Удалим зелёные резисторы R2, R4 и R5 и поставим на их место красные R24, R25 и R45 так, чтобы они обеспечивали такое же омическое поведение элемента R245, а именно, чтобы:

R24 + R25 = [18/11] R ; [4]

R24 + R45 = [30/11] R ; [5]

R25 + R45 = [24/11] R ; [6]

Вычтем из пятого шестое:

R24 – R25 = [6/11] R ;

Сложим это с [4]:

R24 = [12/11] R ;

Из первого:

R25 = [6/11] R ;

Из второго:

R45 = [18/11] R ;

На верхнем левом плече второй эквивалентной схемы: R1 + R25 = [17/11] R ;
На нижнем левом плече второй эквивалентной схемы: R3 + R45 = [40/11] R ;
Значит, ток на верхнем плече второй эквивалентной и исходной схемы будет обратно пропорционален сопротивлению, т.е. будет:

I1 = [40/57] I ;

Обобщая:

I4/I1 = ( [5/19] I ) / ( [40/57] I ) = 3/8 ;

I4 = [3/8] I1 = [3/8]*4 = 1.5 А;

ОТВЕТ: 1.5 А.

Скачать вложение Adobe Acrobat (PDF)