Найдем производную данной функции:
f'(x)=3x²-2x-1
Найдем где производная больше нуля, а где меньше, ведь где производная больше нуля, там функция возрастает, а где меньше - убывает.
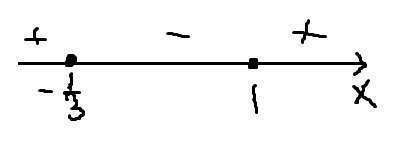
3x²-2x-1=3(x-1)(x+1/3)
(см. вложение)
Значит, если x∈(-∞;-1/3]∪[1;+∞), то функция возрастает, если x∈(-1/3;1), то функция убывает.