Запишем уравнение в виде:
r(t) = x(t)·i + y(t)·j+z(t)·k
Имеем:
x(t) = sin (0,16·t) x(6) = 0,82
y(t) = cos²(0,16·t) y(6) = 0,33
z(t) = 0
Делаем вывод, что точка движется в плоскости ХОY
Скорость - первая производная от координаты.
Имеем:
Vx(t) = 0,16·cos (0,16·t)
Vx(6) = 0,16·cos (0,16·6) ≈ 0,09 м/с
Vy(t) = -2·0,16·cos(0,16·t)·sin (0,16·t) = -0,16·sin(0,32·t) - двойной угол.
Vy(6) = -0,16·sin (0,32·6) ≈ - 0,15 м/с
V=√(0,09²+(-0,15)² )= 0,17 м/с
Ускорение - производная от скорости;
ax(t) = -0,16²·sin (0,16·t)
ax(6) = -0,16²·sin (0,16·6) ≈ 0,002 м/с2
ay(t) = -0,16·0,32·sin (0,32·t)
ay(6) = -0,16·0,32·cos (0,32·6) ≈ - 0,018 м/с²
a=√(0,002²+(-0,018)² )= 0,018 м/с²
Находим траекторию:
sin²(0,16)=x²
cos²(0,16)=y
Сложим:
1=x²+y
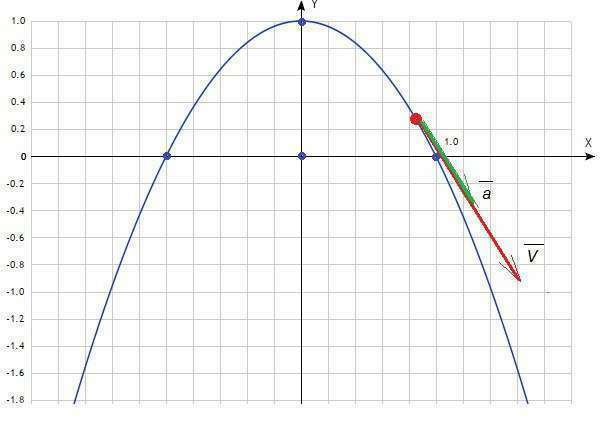
y=1-x² - уравнение ПАРАБОЛЫ.
График смотри в скрине