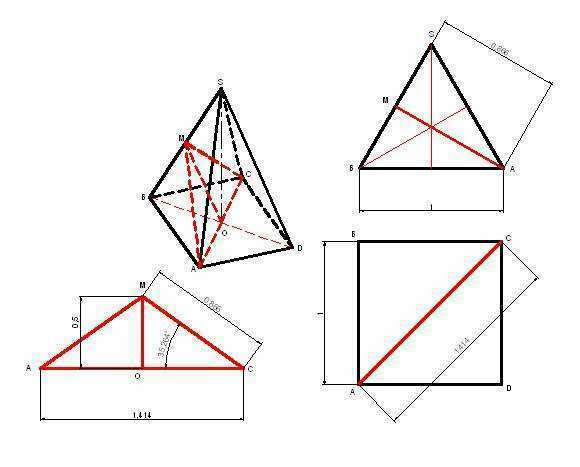
Для нахождения синуса угла между прямой AC и плоскостью SBC надо найти проекцию этой прямой на плоскость SBC.
Боковые грани - равносторонние треугольники со сторонами по 1.
АМ - это перпендикуляр к
SB и равен корень(1^2-(1/2)^2) = V3/2.
Искомый угол - АСМ.
Для нахождения синуса этого угла можно использовать треугольник ОМС.
АС = V2, а ОС = V2/2. ОМ = V((
V3/2)^2 - (V2/2)^2) = 1/2 = 0.5.
MC = AM = V3/2.
Tогда sin ACM = sin OCM = (1/2) /
V3/2. = 1 / V3 = 0.57735.