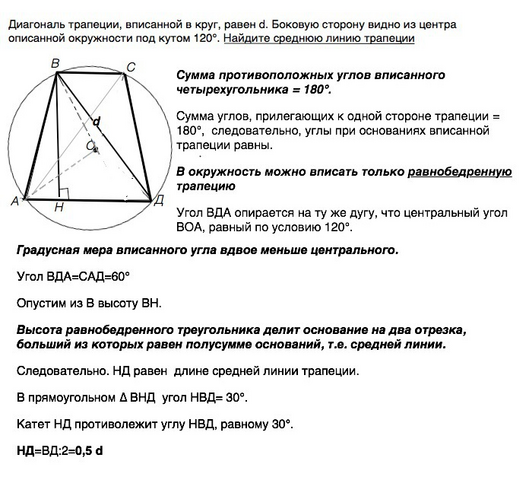
Сумма противоположных углов вписанного четырехугольника = 180°.
Сумма углов, прилегающих к одной стороне трапеции = 180°, следовательно, углы при основаниях вписанной трапеции равны.
В окружность можно вписать только равнобедренную трапецию
Сделаем рисунок и обозначим вершины трапеции АВСД.
ВС - меньшее основание. Центр окружности - О.
Угол ВДА опирается на ту же дугу, что центральный угол ВОА, равный по условию 120°.
Градусная мера вписанного угла вдвое меньше центрального.
Угол ВДА=САД=60°
Опустим из В высоту ВН.
Высота равнобедренного треугольника делит основание на два отрезка, больший из которых равен полусумме оснований, т.е. средней линии.
НД= длине средней линии трапеции.
В прямоугольном ∆ ВНД угол НВД= 30°.
Катет НД противолежит углу НВД, равному 30°.
НД=ВД:2=0,5 d