Врач после осмотра больного считает, что возможно одно из двух заболеваний М или N,...

Question

82 просмотров

Врач после осмотра больного считает, что возможно
одно из двух заболеваний М или N, причем степень своей уве-ренности в отношении правильности диагноза он оценивает как
40 и 60% соответственно. Для уточнения диагноза больного
направляют на анализ, результат которого дает положительную
реакцию при заболевании M в 90% случаев, а при N – 20%.
Анализ дал положительную реакцию. Как изменится мнение
врача после этого?

Математика Rishatmma_zn (12 баллов) 08 Май, 18 | 82 просмотров

Дан 1 ответ

ZolVas_zn · Answer 1 · 2018-05-08T02:52:51+0000

Задача с такими же условиями присутствовала в Интернете, можно поискать (там подробнее).
Тем не менее вот решение.
Решается задача по формуле Байеса.

Прежде всего, уверенность врача в отношении заболеваний M и N составляет, так называемую, полную группу событий (40% + 60% = 100%), то есть у пациента либо заболевание M, либо N.
Это значит, и после проведения исследования вероятности должны составлять 100%.

Итак, пусть $A$ — положительный результат проведённого анализа.
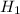$H_1$ — гипотеза, что у пациента болезнь M, тогда $P(H_1|A)$ — вероятность, что у пациента болезнь M после получения информации о положительности результатов анализа.
$H_2$ — гипотеза, что у пациента болезнь N, тогда $P(H_2|A)$ — вероятность, что у пациента болезнь N после получения информации о положительности результатов анализа.

Применим формулу Байеса
$P(H_1|A) = \frac{0,4 * 0,9}{0,4 * 0,9 + 0,6 * 0,2} = \frac{0,36}{0,48} = 0,75$ — вероятность, что у пациента болезнь N.
$P(H_2|A) = \frac{0,6 * 0,2}{0,4 * 0,9 + 0,6 * 0,2} = \frac{0,12}{0,48} = 1 - 0,75 = 0,25$ — вероятность, что у пациента болезнь M.

Итого:
теперь врач должен придавать болезни M вероятность в 0,75, или в 75%,
а болезни N — вероятность в 0,25, или в 25%.