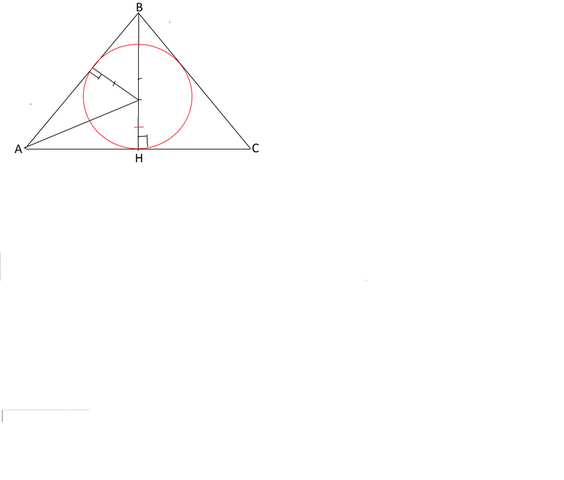Периметр равнобедренного треугольника равен 96 см, а основание и высота, опущенная на него, относятся как 3:2. Точка на медиане, проведенной к основанию, равноудалена от боковой стороны и основания.
Вычислите это расстояние. Найдите площадь вписанной в треугольник окружности.
Медиана равнобедренного треугольника - еще и биссектриса и высота.
Точка на медиане, проведенной к основанию, равноудаленная от боковой стороны и основания - центр вписанной окружности, так как лежит на биссектрисе.
Расстояние от него до основания и стороны -
радиус вписанной окружности.
Сделаем рисунок и рассмотрим
прямоугольный треугольник АВН,
где половина основания АН и высота ВН исходного - катеты, боковая сторона АВ - гипотенуза.
Из отношения высоты и основания
2:3
отношение высоты и половины основания
2:1,5
Пусть коэффициент этого отношения
х
Тогда
АВ²=(2х)²+(1,5х)²=6,25х²
АВ=2,5х
Периметр треугольника 2*2,5х+3х= 8х
х=96:8=
12
АВ=ВС=12*2,5=
30 см
АС=3*12=36 см
Высота ВН=2х=
24см
Радиус вписанной в треугольник окружности равен площади, деленной на полупериметр.
Площадь АВС= ВН*АС:2=24*36:2=432 см²
r=S:p
р=96:2=48
r=432:48=
9 см
S окр=S=πr²=81π см²