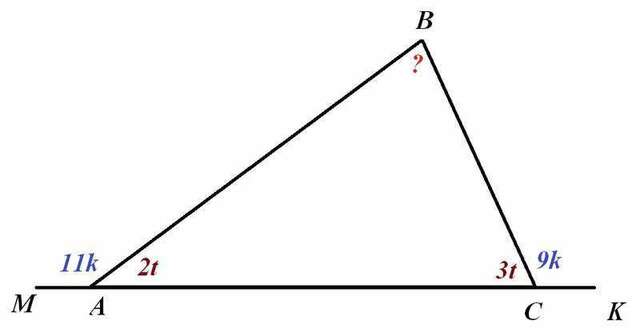
Чертеж во вложении.
Обозначим ∠В=х.
Т.к. ∠ВАС:∠ВСА=2:3, то пусть ∠ВАС=2t, ∠ВСА=3t.
Т.к. ∠МАВ:∠КСВ=11:9, то пусть ∠МАВ=11к, ∠КСВ=9к.
По свойству внешнего угла треугольника получим два равенства:
11k=х+3t
9k=x+2t
По теореме о сумме углов треугольника х=180°-(2t+3t)=180°-5t.
Решаем систему уравнений:
 \begin{cases} t=2k \\ x=180-10k \\ x=11k-3t=11k-6k=5k \end{cases} => \\ 5k=180-10k\\ 15k=180\\ k=12\\\\
\angle B=180^o-10*12^o=60^o" alt="\begin{cases} 11k=x+3t \\9k=x+2t \\ x=180-5t \end{cases} <=> \begin{cases} t=2k \\ x=180-10k \\ x=11k-3t=11k-6k=5k \end{cases} => \\ 5k=180-10k\\ 15k=180\\ k=12\\\\
\angle B=180^o-10*12^o=60^o" align="absmiddle" class="latex-formula">
\begin{cases} t=2k \\ x=180-10k \\ x=11k-3t=11k-6k=5k \end{cases} => \\ 5k=180-10k\\ 15k=180\\ k=12\\\\
\angle B=180^o-10*12^o=60^o" alt="\begin{cases} 11k=x+3t \\9k=x+2t \\ x=180-5t \end{cases} <=> \begin{cases} t=2k \\ x=180-10k \\ x=11k-3t=11k-6k=5k \end{cases} => \\ 5k=180-10k\\ 15k=180\\ k=12\\\\
\angle B=180^o-10*12^o=60^o" align="absmiddle" class="latex-formula">
Ответ: ∠В=60°.